[자료구조] Tree 이론

 

 

 

개념

 

이진 트리

트리 구조(tree)란 그래프의 일종으로, 여러 노드가 한 노드를 가리킬 수 없는 구조이다.

트리는 하나의 최상위 노드를 가지며 이 노드를 노드를 루트 노드(root node)라고 부르며 루트 노드는 0개 이상의 자식 노드를 가지고 있다. 노드 A가 노드 B를 가리킬 때 A를 B의 부모 노드 B를 A의 자식 노드 라고 부르며 자식 노드가 없는 노드를 단말 노드 또는 리프 노드(Leaf node)라고 부른다

 

트리 관련 용어

기본적인 트리

 

노드(node)	트리의 구성요소에 해당하는 A, B, C, D, E, F와 같은 요소
간선(edge)	노드와 노드를 연결하는 연결선
루트 노드(root node)	트리 구조에서 최상위에 존재하는 A와 같은 노드
단말 노드(terminal node, leaf node)	아래로 또 다른 노드가 연결되어 있지 않은 E, F, C, D와 같은 노드
내부 노드(internal node),비 단말 노드(non-terminal node)	단말 노드를 제외한 모든 노드로 A, B와 같은 노드
디그리(degree,차수)	각 노드에서 뻗어나온 가지의 수 A=3, B=2
트리의 디그리	노드들의 디그리 중에서 가장 많은 수 A가 3개의 디그리를 가지기 때문에 트리의 디그리는 3이다.
부모 노드(parent node)	어떤 노드에 연결된 이전 레벨의 노드 E,F의 부모노드는 B
형제 노드(brother node)	동일한 부모를 갖는 노드들 E의 형제노드는 F

레벨과 높이

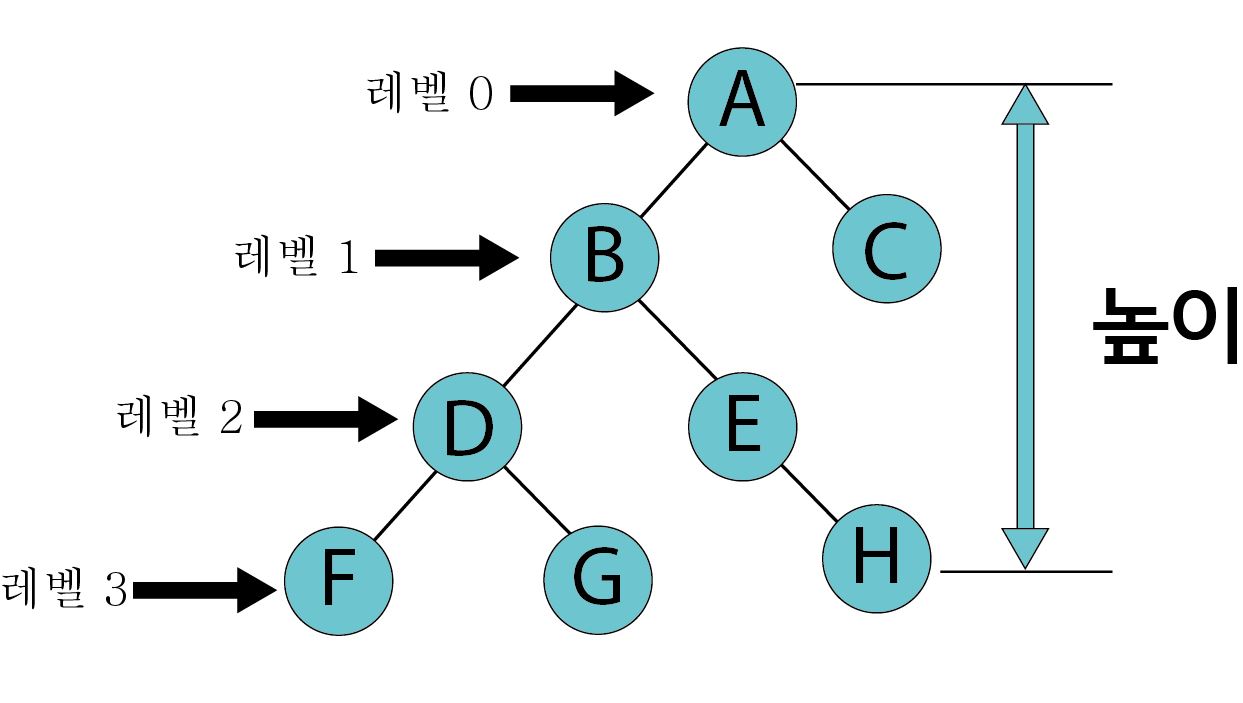
레벨(level),깊이	트리에서의 각 층별로 숫자로 매겨서 이를 트리의 '레벨'이라 한다. 이 트리의 레벨(깊이)는 3이다.
높이(height)	트리의 최고 레벨을 가리켜 '높이'라 한다.

이진 트리

이진 트리의 조건

• 루트 노드를 중심으로 두 개의 서브 트리로 나뉘어진다.
• 나뉘어진 두 서브 트리도 모두 이진 트리이어야 한다.

포화 이진 트리(Full Binary Tree) 와 완전 이진 트리(Complete Binary Tree)

포화 이진 트리

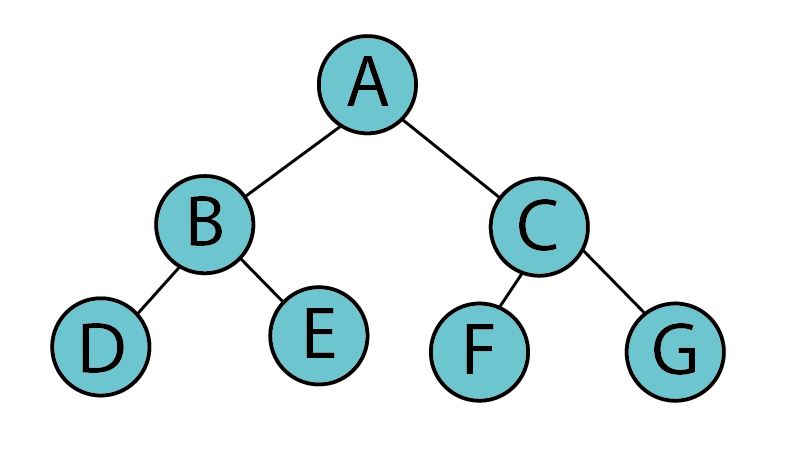
모든 레벨이 꽉 찬 이진 트리를 포화 이진 트리 라고 부른다.

 

완전 이진 트리

포화 이진 트리처럼 모든 레벨이 꽉 찬 상태는 아니지만, 차곡차곡 빈 틈 없이 노드가 채워진 이진 트리를 완전 이진 트리 라고 한다.

 

이진 트리

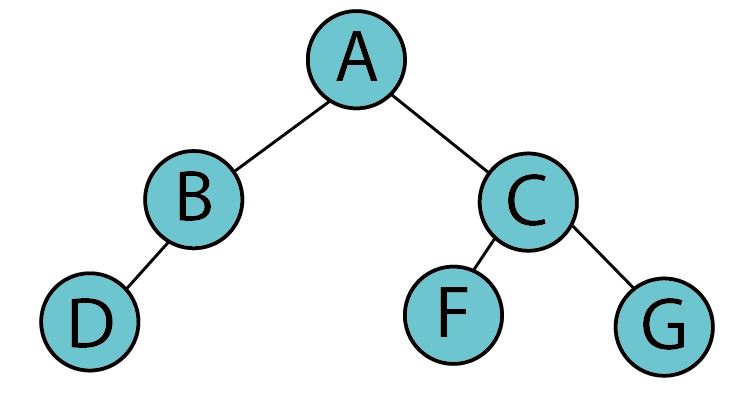
위의 트리도 이진 트리의 조건에 부합한다. 하지만 레벨 2의 가장 왼쪽 위치에 노드가 존재하지 않는 즉 빈 틈이 있는 상태이다. 따라서 '이진 트리'이긴 하되 '완전 이진 트리'는 아니다.

 

트리의 순회

순회에는 세 가지 방법이 있다.

• 전위 순회(Preorder Traversal) 루트 노드를 먼저
• 중위 순회(Inorder Traversal) 루트 노드를 중간에
• 후위 순회(Postorder Traversal) 루트 노드를 마지막에

순회는 이렇게 루트 노드를 언제 방문하느냐에 따라 나뉘게 된다.

 

전위 탐색

A->B->C 순으로 순회를 진행한다.

중위 탐색

B->A->C 순으로 순회를 진행한다.

후위 탐색

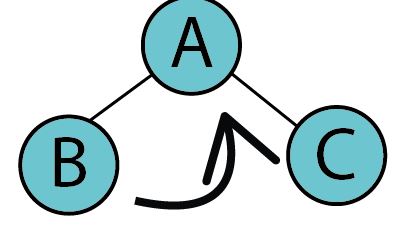
B->C->A 순으로 순회를 진행한다.

 

출처 및 레퍼런스

Wiki: https://ko.wikipedia.org/wiki/트리_구조

윤성우의 열혈 자료구조: http://www.orentec.co.kr/teachlist/DA_ST_1/teach_sub1.php

그림: 본인