자료구조
컴퓨터 과학에서, 우선순위 큐는 평범한 큐나 스택과 비슷한 축약 자료형이다. 우선순위 큐는 각 원소들이 우선순위를 가지고 있다.
우선순위 큐를 구현하는 방법에는 세 가지가 있다
1. 배열을 기반으로 구현하는 방법
2. 연결 리스트를 기반으로 구현하는 방법
3. 힙(heap)을 이용하는 방법
배열을 이용한 방법의 경우에는 두 가지의 단점이 있다.
1. 데이터를 삽입 삭제하는 과정에서 데이터를 한 칸씩 뒤로 밀거나 한 칸씩 앞으로 당기는 연산이 들어가는 문제 이는 배열의 대표적인 단점이다.
2. 삽입의 위치를 찾기 위해서 배열에 저장된 모든 데이터와 우선순위의 비교를 진행해야 할 수 있는 문제
연결 리스트 기반으로 구현하는 방법도 2번의 단점을 가진다.
그래서 우선순위 큐는 단순 배열도 연결 리스트도 아닌 "힙"이라는 자료구조를 이용해서 구현하는 것이 일방적이다.
또한 우선순위 큐 가 힙이라는 것은 잘못된 상식이며 우선순위 큐는 "리스트"나 "맵"과 같이 추상적인 개념이며 힙이나 다양한 방법으로 구현을 할 수 있다.
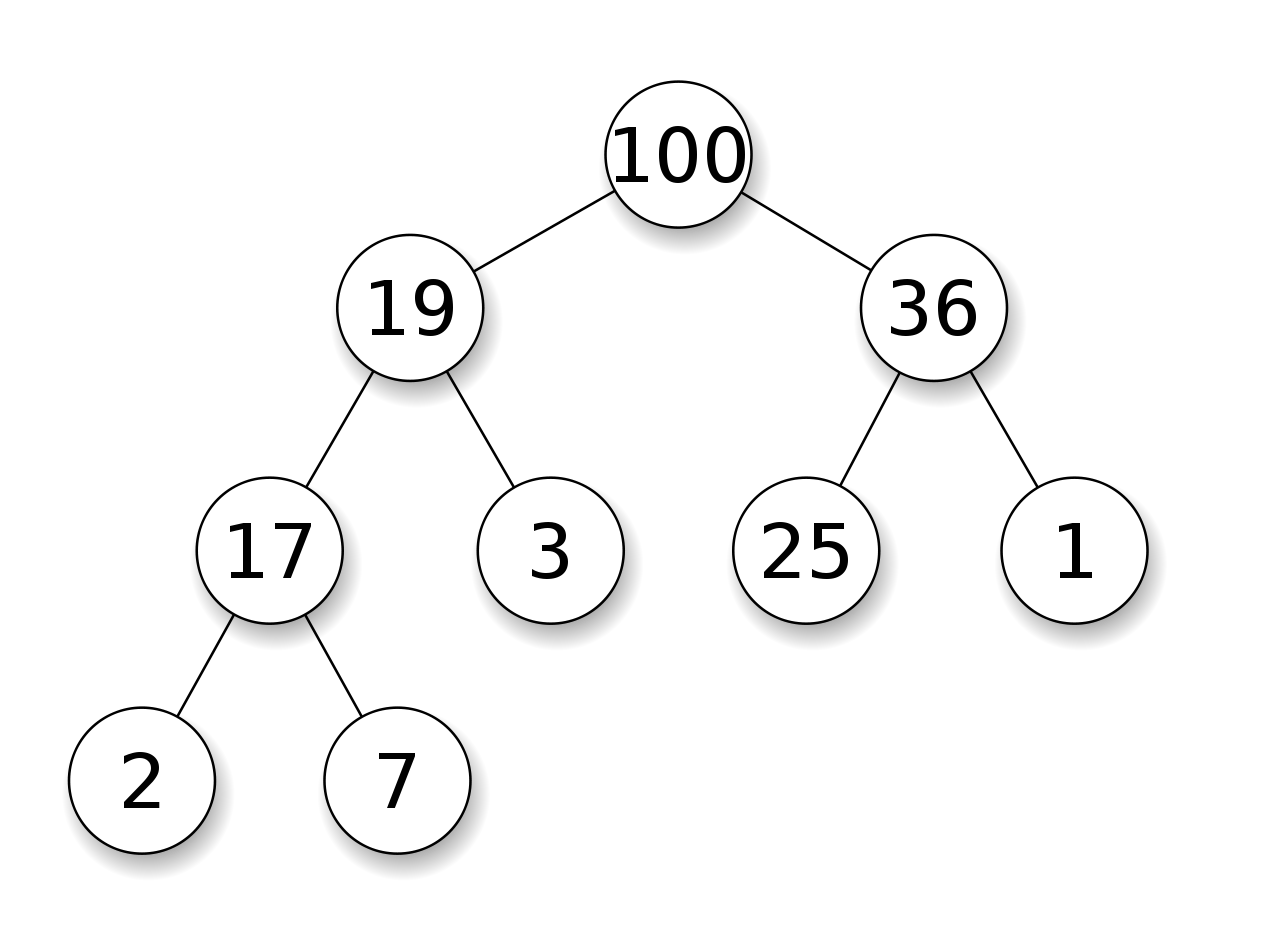
힙의 삽입 삭제
힙은 이진트리 이되 완전 이진트리이다. 그리고 모든 노드에 저장된 값은 자식 노드에 저장된 값보다 크거나 같아야 한다. 즉 루트 노드에 저장된 값이 가장 커야 한다.

힙의 데이터 추가 과정은 마지막 위치에 데이터를 두고서 부모 노드와의 비교를 통해 자신의 위치를 찾아가는 방식이다.
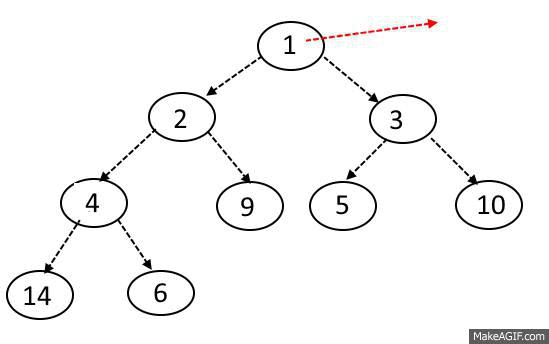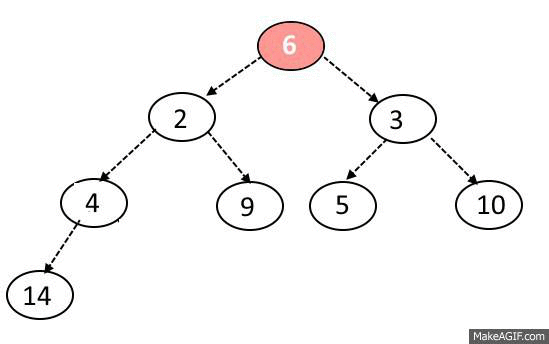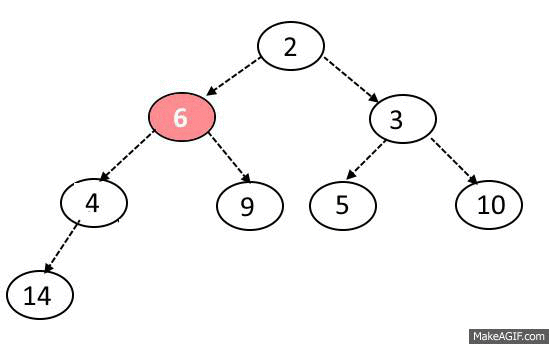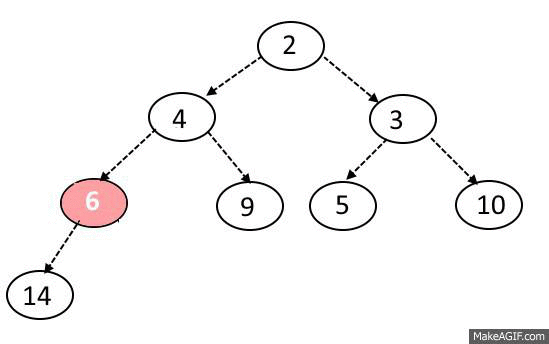
힙의 데이터 삭제 과정은 마지막 위치에 있던 데이터를 루트 노드로 옮긴 후 왼쪽 오른쪽 자식 노드와 비교 후 우선순위가 더 높은 노드와 교환을 진행한다. 여기서 우선순위가 낮은 노드와 교환을 진행할 경우 힙의 기본 조건이 무너지게 된다.
어느 자료구조가 적합한가?
| 자료구조 | 시간 복잡도 |
| 배열의 삽입/삭제 | O(N)/O(1) |
| 연결리스트의 삽입/삭제 | O(N)/O(1) |
| 힙의 삽입/삭제 | O(logn)/O(logn) |
배열과 연결리스트 기반의 경우 저장된 모든 데이터와 우선순위를 비교해야 하기 때문에 O(N)이며 삭제의 경우 가장 앞의 데이터를 삭제하기 때문에 O(1)의 시간 복잡도를 가진다.
힙의 경우에는 삽입 삭제의 연산이 주로 부모 노드와 자식 노드 사이에 일어나기 때문에 트리의 높이에 해당하는 수만큼만 비교 연산을 진행하면 되기 때문에 O(logn)의 시간 복잡도를 가진다.
이 사실을 통해 우선순위 큐를 구현하기에 적합한 것은 힙이라는 것을 알 수 있다.
소스코드
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
|
#pragma once
#include<iostream>
typedef bool BOOL;
typedef int PriorityComp(int lhs, int rhs);
constexpr int MAX = 1000;
/*
1부터 시작
왼쪽 자식= 부모노드 *2
오른쪽 자식= 부모노드*2 +1
부모 노드= 자식노드/2
*/
template<class T>
class pPriority_Queue {
enum class FunctionType { HIGH = 0, LOW };
private:
struct Node {
bool is_data;
T data;
};
Node node_[MAX];
size_t size_;
size_t level_;
private:
void Enqueue(const T value_, int index) {
if (node_[index].is_data == false) {
node_[index].data = value_;
node_[index].is_data = true;
FindPosition(index, FunctionType::LOW);
++size_;
return;
}
else if (node_[index * 2].is_data == false)
Enqueue(value_, index * 2);
else if (node_[(index * 2) + 1].is_data == false)
Enqueue(value_, (index * 2) + 1);
else
Enqueue(value_, ++index);
}
void Swap(T& lhs, T& rhs) {
T temp = lhs;
lhs = rhs;
rhs = temp;
}
public:
pPriority_Queue() :size_(0), level_(0) {
for (int i = 0; i < MAX; ++i)
node_[i].is_data = false;
}
/*
Enqueue의 핵심은 최하위로 값을 넣고 하나씩 비교하면서 자리를 찾는다.
*/
void Enqueue(const T&& value_) {
Enqueue(value_, 1);
}
void Enqueue(const T& value_) {
Enqueue(value_, 1);
}
/*
Dequeue의 핵심은 최하위 값을 루트로 올리고 비교하면서 자리를 찾는다.
*/
T Dequeue() {
T rootValue;
if (node_[1].is_data != false)
rootValue = node_[1].data;
node_[1] = node_[size_];
node_[size_] = node_[0];
--size_;
FindPosition(1, FunctionType::HIGH);
return rootValue;
}
/*
HIGH: Enqueue Check
LOW: Dequeue Check
*/
void FindPosition(int index, FunctionType type) {
if (type == FunctionType::LOW) {
while (index > 1) {
int parent = index / 2;
//자식노드 값의 우선순위가 더 높다면 루트노드와 바꾼다.
if (node_[index].data > node_[parent].data) {
Swap(node_[index].data, node_[parent].data);
index = parent;
parent = index / 2;
}
else
break;
}
}
else if (type == FunctionType::HIGH) {
//위에서 부터 아래로 내려간다. 자식노드가 없을 때 까지
while (int swapIndex = GetHiNodeIndex(index)) {
//자식노드가 더 크다.
if (node_[index].data < node_[swapIndex].data) {
Swap(node_[index].data, node_[swapIndex].data);
index = swapIndex;
}
else
break;
}
}
}
int GetHiNodeIndex(int index) {
int left = index * 2;
int right = index * 2 + 1;
// 자식이 둘 있는경우
if (node_[left].is_data && node_[right].is_data) {
if (node_[left].data>node_[right].data) {
return left;
}
else
return right;
}
// 자식이 Left만 있는경우
else if (node_[left].is_data && node_[right].is_data == false) {
return left;
}
//자식이 없는경우
else if (!node_[left].is_data && !node_[right].is_data) {
return 0;
}
}
void DisplayAll() {
size_t saveSize = size_;
for (size_t i = 1; i <= saveSize; ++i) {
T data = Dequeue();
std::cout<<data << " ";
}
std::cout << "\n";
}
size_t Size()const { return size_; }
size_t Memory()const { return sizeof(node_); }
};
|
후기
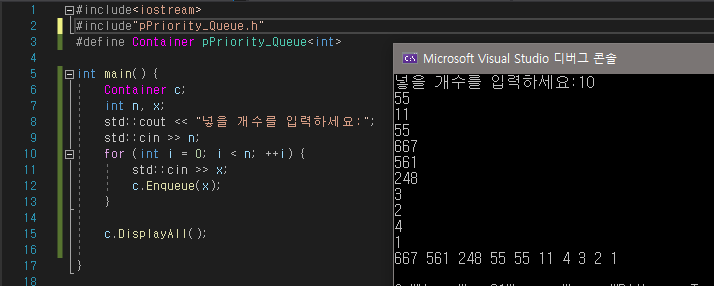
우선순위 큐를 구현해보았다. 힙을 연결 리스트가 아닌 배열로 구현을 했는데 보통 일반적으로 배열을 이용해서 구현을 한다고 한다. 다음에는 우선순위 큐 문제를 풀 예정이다.
출처 및 레퍼런스
Wiki: https://ko.wikipedia.org/wiki/우선순위_큐
gif: https://algorithms.tutorialhorizon.com/binary-min-max-heap/
윤성우의 열혈 자료구조: http://www.orentec.co.kr/teachlist/DA_ST_1/teach_sub1.php
2020.03.09: 코드 오류 수정
문제 관련 글
[온라인 코딩/힙(Heap)] - [백준] 11279번 최대 힙
'자료구조 알고리즘 > 큐(Queue)와 스택(Stack)' 카테고리의 다른 글
| [자료구조] 간단한 Queue 구현 (1) | 2019.12.16 |
|---|---|
| [자료구조] 간단한 Stack 구현 (1) | 2019.12.15 |

