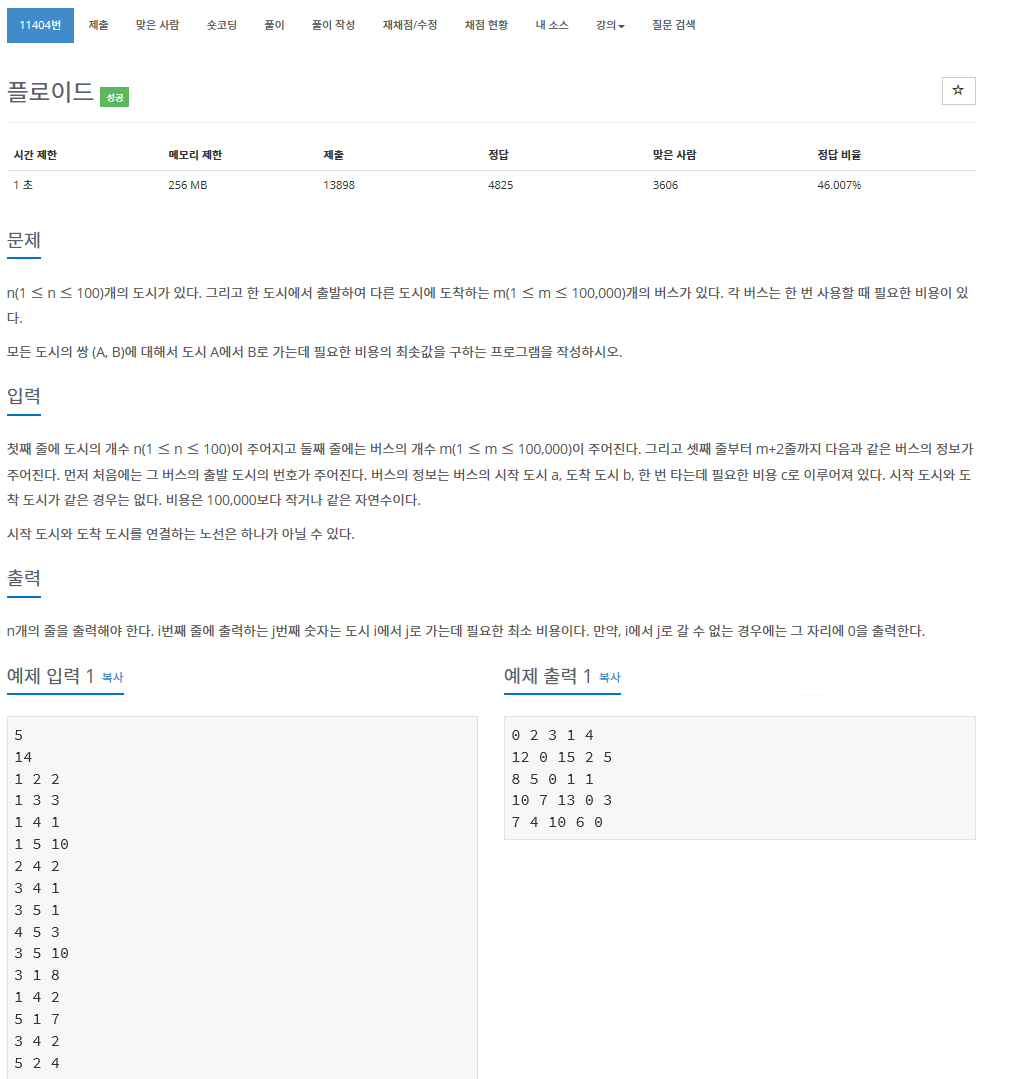
문제
소스코드
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
|
#include<iostream>
constexpr int MAX_N = 101;
constexpr int MAX_M = 10000001;
int g_graph[MAX_N][MAX_N];
void DisplayAll(int node_count) {
for (int i = 1; i <= node_count; ++i) {
for (int j = 1; j <= node_count; ++j) {
if (g_graph[i][j] == MAX_M) {
std::cout << "0 ";
}
else
std::cout << g_graph[i][j] << " ";
}
std::cout << "\n";
}
}
void MakeSet(int node_count) {
for (int i = 1; i <= node_count; ++i) {
for (int j = 1; j <= node_count; ++j) {
if(i!=j)
g_graph[i][j] = MAX_M;
}
}
}
void FloyedWarshall(int node_count) {
// k: 중간 정점 집합
// i: 시작 정점
// j: 마지막 정점
// MIN( [i][j],[i][k]+[k][j] )
for (int k = 1; k <= node_count; ++k) {
for (int i = 1; i <= node_count; ++i) {
for (int j = 1; j <= node_count; ++j) {
if (g_graph[i][j] > g_graph[i][k] + g_graph[k][j]) {
g_graph[i][j] = g_graph[i][k] + g_graph[k][j];
}
}
}
}
}
int main() {
int N, M;
int from_v, to_v, weight;
std::cin >> N >> M;
//모든 경로를 INF로 설정
MakeSet(N);
//정보 입력
for (int i = 0; i < M; ++i) {
std::cin >> from_v >> to_v >> weight;
//더 작은 간선 정보로 바꾼다.
if (g_graph[from_v][to_v] > weight) {
g_graph[from_v][to_v] = weight;
}
}
//플로이드-와샬 알고리즘 실행
FloyedWarshall(N);
//출력
DisplayAll(N);
}
|
후기
이 문제를 해결하기 위한 키워드는 다음과 같다.
*플로이드-워샬 알고리즘을 사용해서 모든 정점의 최단 경로를 찾는다.
FloyedWarshall()메소드에 구현을 진행하였다.
*플로이드-워샬이란 플로이드(Floyd)와 워샬(Warshall)의 이름을 따온 것이며 모든 정점 사이의 최단 거리를 구할 수 있다는 특징이 있다. 플로이드-워샬은 동적 프로그래밍의 원리를 사용하면서 O(N^3)의 시간 복잡도를 가진다.
플로이드 워샬의 진행 순서는 다음과 같다.
1. 자기 자신의 경로를 제외한 모든 경로를 INF(무한)으로 설정한다.
2. 정점을 경유해서 가는 경우와 바로 가는 경우를 비교해서 정점을 경유해서 가는 경우가 더 가깝다면 바꾼다.
D[i][j] <- min {D [i][j], D [i][k]+D [k][j] } k: 중간 정점, i: 시작 정점, j: 마지막 정점
3. 위 내용을 반복한다.
* 추가적으로 이 문제에서 시작 도시에서 도착 도시의 노선이 하나가 아닐 수 있다는 경우가 존재하기 때문에 입력을 받으면서 입력을 받은 가중치가 더 작다면 해당 경로로 바꾸는 로직을 추가하였다.
출처 및 레퍼런스
문제 링크:https://www.acmicpc.net/problem/11404
Book: 쉽게 배우는 알고리즘 문병로 저
'온라인 코딩 > 탐색(Search)' 카테고리의 다른 글
| [백준] 15649번 N과 M (0) | 2020.04.02 |
|---|---|
| [구름 IDE] 비타알고 시즌3 백신(★3) (0) | 2020.03.27 |
| [백준] 1717번 집합의 표현 (0) | 2020.03.25 |
| [백준] 2798번 블랙잭 (0) | 2020.03.24 |
| [구름 IDE] 비타알고 시즌2 학교 지도 만들기(★3) (0) | 2020.03.17 |



