[알고리즘] CCW(Counter Clock Wise)

알고리즘 개요 및 소개

CCW( Counter Clock Wise) 알고리즘은 3개의 점 A, B, C가 있을 때 이 점 3개를 이은 직선의 방향을 알고자 할 때 유용한

기하 알고리즘이다.

경우의 수는 총 3가지가 있으며 시계, 반시계, 직선이 있으며 이는 외적을 통하여 구할 수 있으며 외적의 결과가 음수이면 시계 방향, 직선은 0, 반시계 방향일 경우 양수가 나오게 된다.

외적의 정의 및 특징

외적: 두 개의 3차원 공간상의 벡터에 대한 연산

외적은 다음과 같은 특징이 있다.

기호로는 X를 사용한다
두 벡터를 외적 하면 두 벡터의 수직 벡터 즉 벡터가 나온다 내적은 스칼라 값이 나온다.
외적은 교환 법칙이 성립하지 않는다. a x b와 b x a는 다르다.
두 벡터의 외적은 두 벡터가 만들어내는 평행사변형의 넓이이다.

또한 행렬을 통해서 외적을 구할 수 있는대 방법은 아래와 같다.

외적의 정의 및 특징에 대해서 간략하게 작성을 진행하였다. 자세한 내용은 검색을 통하는 것을 추천한다.

오른손 법칙을 통한 방향 알아내기

두 벡터를 외적 했을 때의 방향을 알아내는 방법은 오른손 법칙을 사용하는 것이다.

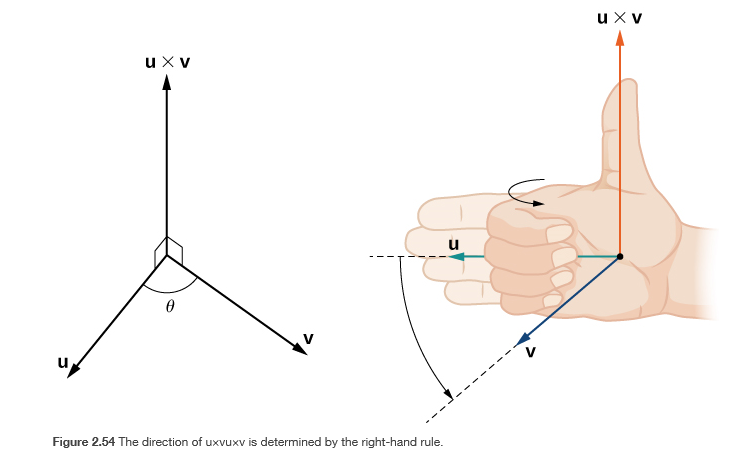
오른손으로 해당하는 방향으로 쥐었을 때의 엄지 방향이 그 수직 벡터의 방향이 된다. 이 그림에서는 u x v이기 때문에

u벡터에서 v 벡터로 손을 감았을 때 엄지가 위에 있기 때문에 두 벡터의 수직 벡터는 위를 바라보게 된다. 만약에 v x u 였다면 반대로 엄지가 아래를 향하게 된다.

CCW 구하는 방법

위와 같이 점 3개 A, B, C 가 있다는 가정하에 진행을 해보겠다. 점 C를 기준으로 CA와 AB 벡터를 먼저 만든다.

이후 벡터 CA와 AB의 외적을 진행하면 된다. 여기서 2차원이기 때문에 Z값에 0을 넣고 외적을 진행한다.

이후 위에 있는 행렬을 사용하여 외적을 진행하면 z 값이 0이기 때문에 ( 0 , 0 , ad-bc)가 나오게 된다.

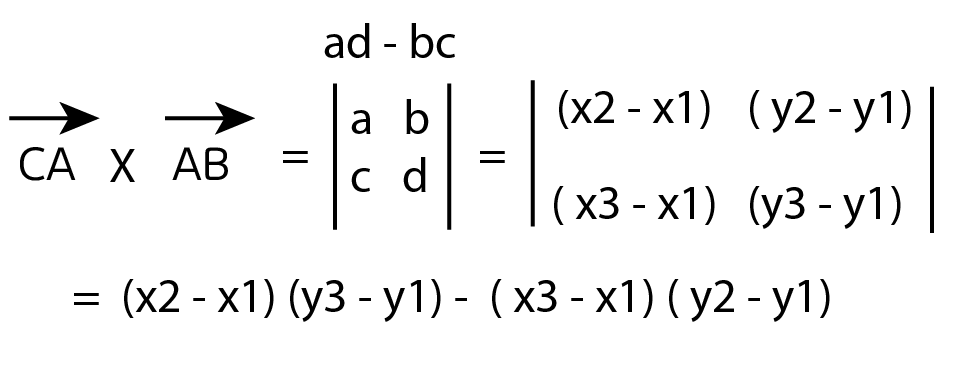
그래서 최종적으로 이러한 공식이 성립이 되고 여기에 벡터 CA와 AB의 값을 넣으면

와 같은 결과가 나오며 값이 양수가 나왔기 때문에 반시계 방향이라는 것을 알 수 있다.

소스코드

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

#include<iostream>
 
struct Point {
private:
public:
    int x;
    int y;
};
 
int CCW(int x1, int y1, int x2, int y2, int x3, int y3) {
    return (x2 - x1) * (y3 - y1) - (x3 - x1) * (y2 - y1);
}
 
 
int main() {
    Point P1, P2, P3;
 
 
    std::cin >> P1.x >> P1.y;
    std::cin >> P2.x >> P2.y;
    std::cin >> P3.x >> P3.y;
 
 
    int result = CCW(P1.x, P1.y, P2.x, P2.y, P3.x, P3.y);
 
    if (result == 0) {
        std::cout << "직선: "<<result<<"\n";
    }
    else if (result > 0) {
        std::cout << "반시계방향: " << result << "\n";
    }
    else {
        std::cout << "시계방향: " << result << "\n";
    }
 
}
 