자료구조
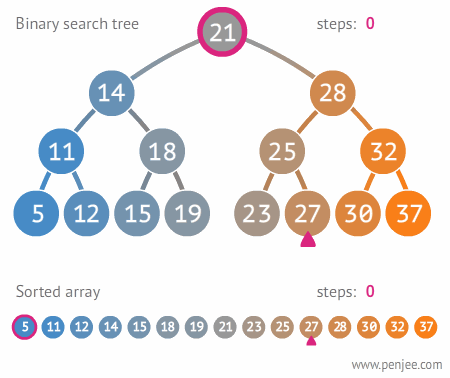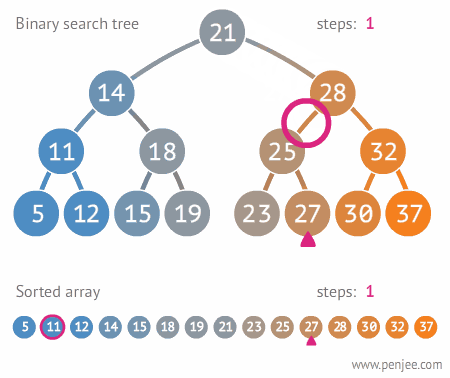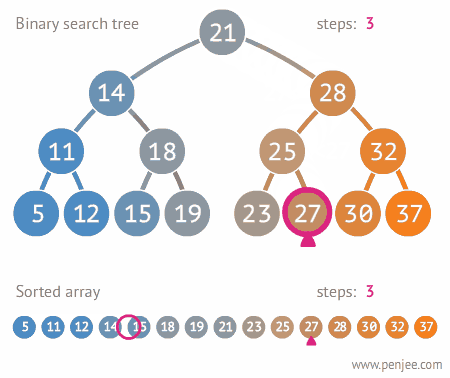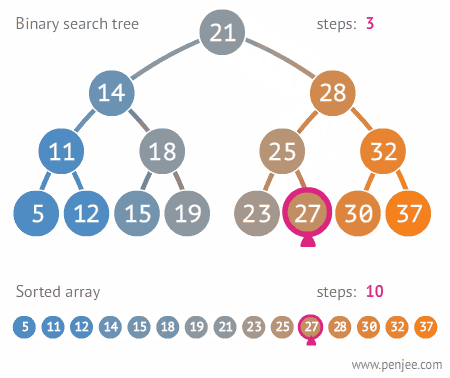
이진트리는 완전 이진트리, 포화 이진트리, 균형 이진트리 등이 있다. 이진 검색 트리는 이진 트리에 몇 가지 조건이 추가된 트리이다.
- 각 노드에 값이 있다.
- 값들은 전 순서가 있다.
- 노드의 왼쪽 서브 트리에는 그 노드보다 작은 값들을 지닌 노드로 이루어져 있다.
- 노드의 오른쪽 서브트리에는 그 노드보다 큰 값들을 지닌 노드로 이루어져 있다.
- 좌우 하위 트리는 각각이 다시 이진 탐색 트리여야 한다.
소스코드
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
|
#pragma once
#include<iostream>
typedef bool BOOL;
template<class T>
class pBinary_Tree {
struct Node;
private:
Node* root_;
size_t size_;
struct Node {
public:
Node* leftChild_;
Node* rightChild_;
T data_ = ;
Node() :data_(-1) {
leftChild_ = rightChild_ = nullptr;
}
Node(const T& data) :data_(data) {
leftChild_ = rightChild_ = nullptr;
};
Node(const T&& data) :data_(data) {
leftChild_ = rightChild_ = nullptr;
};
//root->left->right
Node* InitNode(Node* node, const T& data) {
if (node == nullptr) {
node = new Node(data);
return node;
}
else if (node->data_ > data)
node->leftChild_ = InitNode(node->leftChild_, data);
else if (node->data_ < data)
node->rightChild_ = InitNode(node->rightChild_, data);
return node;
}
//root->left->right
Node* InitNode(Node* node, const T&& data) {
if (node == nullptr) {
node = new Node(data);
return node;
}
else if (node->data_ > data)
node->leftChild_ = InitNode(node->leftChild_, data);
else if (node->data_ < data)
node->rightChild_ = InitNode(node->rightChild_, data);
return node;
}
//전위탐색 root->left->right
void Preorder(Node* node) {
if (node == nullptr)return;
std::cout << node->data_ << " ";
Preorder(node->leftChild_);
Preorder(node->rightChild_);
}
//중위탐색 left->root->right
void Inorder(Node* node) {
if (node == nullptr)return;
Inorder(node->leftChild_);
std::cout << node->data_ << " ";
Inorder(node->rightChild_);
}
//후위탐색 left->right->root
void PostOrder(Node* node) {
if (node == nullptr)return;
PostOrder(node->leftChild_);
PostOrder(node->rightChild_);
std::cout << node->data_ << " ";
}
//Preorder Search
bool SMP(Node* node, int data) {
if (node != nullptr && node->data_ == data)
return true;
else {
if (node != nullptr && node->data_ < data)
return SMP(node->rightChild_, data);
else if (node != nullptr && node->data_ > data)
return SMP(node->leftChild_, data);
else
return false;
}
}
Node* DeleteNode(Node* node, int data) {
//Find Node
if (node != nullptr && node->data_ == data) {
Node* temp = node;
Node* left = node->leftChild_;
Node* right = node->rightChild_;
//자식 노드 두개를 가지고 있는 경우 오른쪽에서 작은값을 root로 지정
if (left && right) {
Node* newNode = nullptr;
if (right->leftChild_ == nullptr) {
newNode = right;
newNode->leftChild_ = left;
newNode->rightChild_ = right->rightChild_;
}
else {
newNode = FindMinNode(right);
newNode->rightChild_ = right;
newNode->leftChild_ = left;
}
delete temp;
return newNode;
}
//left는 있고 right가 없는경우
else if (left != nullptr && right == nullptr) {
delete temp;
return left;
}
//right는 있고 left가 없는경우
else if (left == nullptr && right != nullptr) {
delete temp;
return right;
}
//단말(리프)노드의 경우
else {
delete temp;
return nullptr;
}
}
if (node != nullptr && node->data_ < data)
node->rightChild_ = DeleteNode(node->rightChild_, data);
else if (node != nullptr && node->data_ > data)
node->leftChild_ = DeleteNode(node->leftChild_, data);
return node;
}
Node* FindMinNode(Node* node) {
Node* nextNode = node->leftChild_;
//왼쪽노드가 nullptr가 아니면 계속 순환
while (nextNode->leftChild_ != nullptr) {
node = node->leftChild_;
nextNode = node->leftChild_;
}
node->leftChild_ = nullptr;
return nextNode;
}
};
public:
pBinary_Tree() :size_(0) {
root_ = new Node();
root_ = nullptr;
}
void InitNode(const T& data) {
root_ = root_->InitNode(root_, data);
}
void InitNode(const T&& data) {
root_ = root_->InitNode(root_, data);
}
//전위탐색 root->left->right
void Preorder()const {
if (root_ == nullptr)return;
std::cout << "Preorder Search: ";
root_->Preorder(root_);
std::cout << "\n";
}
//중위탐색 left->root->right
void Inorder()const {
if (root_ == nullptr)return;
std::cout << "Inorder Search: ";
root_->Inorder(root_);
std::cout << "\n";
}
//후위탐색 left->right->root
void PostOrder()const {
if (root_ == nullptr)return;
std::cout << "PostOrder Search: ";
root_->PostOrder(root_);
std::cout << "\n";
}
//Search Money Player
bool SMP(int data)const {
return root_->SMP(root_, data);
}
//Delete Node(Player)
void DeleteNode(int data) {
root_=root_->DeleteNode(root_, data);
}
};
|
함수
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
|
//root->left->right
Node* InitNode(Node* node, const T& data) {
if (node == nullptr) {
node = new Node(data);
return node;
}
else if (node->data_ > data)
node->leftChild_ = InitNode(node->leftChild_, data);
else if (node->data_ < data)
node->rightChild_ = InitNode(node->rightChild_, data);
return node;
}
//root->left->right
Node* InitNode(Node* node, const T&& data) {
if (node == nullptr) {
node = new Node(data);
return node;
}
else if (node->data_ > data)
node->leftChild_ = InitNode(node->leftChild_, data);
else if (node->data_ < data)
node->rightChild_ = InitNode(node->rightChild_, data);
return node;
}
|
<삽입 부분>





삽입은 재귀함수를 이용해서 구현했으며 반복문으로도 구현이 가능하다.
|
1
2
3
4
5
6
7
|
//전위탐색 root->left->right
void Preorder(Node* node) {
if (node == nullptr)return;
std::cout << node->data_ << " ";
Preorder(node->leftChild_);
Preorder(node->rightChild_);
}
|
<탐색 부분>

전위탐색은 Root->Left->Right순으로 탐색이 진행된다. 처음 50(root)을 탐색 후 26(Left)으로 내려간다. 여기서 26(Left)은 서브 트리의 root이기 때문에 25(Left)로 내려가고 동일하게 10->5를 탐색 후 20(Right)을 탐색 후 40->35->30을 지나 50(root)의 오른쪽을 동일하게 탐색한다.
중위 탐색은 Left->Root->Right, 후위 탐색은 Left->Right->Root 순이다. Root를 기준으로 전중후가 정해진다고 보면 쉽다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
|
Node* DeleteNode(Node* node, int data) {
//Find Node
if (node != nullptr && node->data_ == data) {
Node* temp = node;
Node* left = node->leftChild_;
Node* right = node->rightChild_;
//자식 노드 두개를 가지고 있는 경우 오른쪽에서 작은값을 root로 지정
if (left && right) {
Node* newNode = nullptr;
if (right->leftChild_ == nullptr) {
newNode = right;
newNode->leftChild_ = left;
newNode->rightChild_ = right->rightChild_;
}
else {
newNode = FindMinNode(right);
newNode->rightChild_ = right;
newNode->leftChild_ = left;
}
delete temp;
return newNode;
}
//left는 있고 right가 없는경우
else if (left != nullptr && right == nullptr) {
delete temp;
return left;
}
//right는 있고 left가 없는경우
else if (left == nullptr && right != nullptr) {
delete temp;
return right;
}
//단말(리프)노드의 경우
else {
delete temp;
return nullptr;
}
}
if (node != nullptr && node->data_ < data)
node->rightChild_ = DeleteNode(node->rightChild_, data);
else if (node != nullptr && node->data_ > data)
node->leftChild_ = DeleteNode(node->leftChild_, data);
return node;
}
Node* FindMinNode(Node* node) {
Node* nextNode = node->leftChild_;
//왼쪽노드가 nullptr가 아니면 계속 순환
while (nextNode->leftChild_ != nullptr) {
node = node->leftChild_;
nextNode = node->leftChild_;
}
node->leftChild_ = nullptr;
return nextNode;
}
|
<삭제 부분>
삭제는 3가지의 경우가 있다.
1. 자식 노드 두개를 모두 가지고 있는 경우
2. 한쪽 노드만 가지고 있는 경우
3. 단말(리프)노드인 경우
1번의 경우에는 두 가지 방법이 있는대 왼쪽에서 가장 큰 값을 root로 올리는 방법과 오른쪽에서 가장 작은 값을 root로 올리는 방법이다. 여기서는 후자의 방법을 사용했으며 Data가 아닌 Pointer의 교환으로 인해 교환으로 인한 오버헤드를 최소화하였다. 지금은 Data크기가 작아서 큰 문제가 없지만 Player Class에는 Level, HP, MP, EXP 등 다양한 변수가 모듈화 되어있고 그 자료구조를 교환하는 것은 큰 오버헤드이기 때문에 가리키는 메모리 주소만 스왑 하게 구현하였다.
3번은 자기자신이 삭제되기 때문에 nullptr을 반환해서 부모 노드가 nullptr를 가리키게 만든다.
후기
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
|
int main() {
Container container;
container.InitNode(Player(50));
container.InitNode(Player(26));
container.InitNode(Player(63));
container.InitNode(Player(90));
container.InitNode(Player(40));
container.InitNode(Player(25));
container.InitNode(Player(35));
container.InitNode(Player(60));
container.InitNode(Player(10));
container.InitNode(Player(20));
container.InitNode(Player(5));
container.InitNode(Player(30));
container.Preorder();
container.Inorder();
container.PostOrder();
std::random_device rnd;
std::mt19937 mt(rnd());
std::uniform_int_distribution<int> dist(0, INT_MAX);
std::unordered_set<int>u_set;
for (int i = 0; i < 10000000;) {
int value = dist(mt);
if (u_set.count(value)==false) {
//std::cout << i << "\n";
u_set.insert(value);
container.InitNode(Player(value));
++i;
}
}
int money = 30;
//해당하는 돈을가진 플레이어가 있는지 찾는다.
system_clock::time_point start = system_clock::now();
if (container.SMP(money)) {
std::cout << "돈을"<< money <<"가진 플레이어가 있습니다." << std::endl;
}
else {
std::cout << "돈을" << money << "가진 플레이어가 없습니다." << std::endl;
}
duration<double> sec = system_clock::now() - start;
std::cout << "Elapsed Time:" << sec.count() << "sec" << std::endl;
container.DeleteNode(money);
if (container.SMP(money)) {
std::cout << "돈을" << money << "가진 플레이어가 있습니다." << std::endl;
}
else {
std::cout << "돈을" << money << "가진 플레이어가 없습니다." << std::endl;
}
}
|

제네릭한 이진 검색 트리를 만들었다. 중복이 허용되는 이진트리도 있다고 하는데 메커니즘은 노드에 연결 리스트를 붙이면 되는 거라 어려워 보이지는 않았다. 중복이 없는 랜덤 값을 만들다 보니 unordered_set을 사용했다.
돈은 중복도 생기기 때문에 어울리지는 않지만 억지로 넣어서 돌려봤다.
출처 및 레퍼런스
Wiki: https://ko.wikipedia.org/wiki/이진_탐색_트리
Gif: https://medium.com/swlh/how-to-solve-a-js-binary-search-tree-problem-585673fc3287
2020.01.30
Root노드 삭제 불가능한 오류 수정
20.04.22
소스코드 -> color Scripter, 글자 폰트 및 색상 변경
'자료구조 알고리즘 > 그래프(Graph)와 트리(Tree)' 카테고리의 다른 글
| [자료구조] 그래프(Graph) (0) | 2020.02.06 |
|---|
