자료구조

그래프 알고리즘은 수학자 '오일러Euler)'에 의해 고안되었다. 오일러는 1736년도에 '쾨니히 스베르크의 다리 문제'를 풀기 위해서 그래프 이론을 사용하였다고 한다. 그래프 이론의 역사는 수백 년에 이르지만 컴퓨터 분야에 활용하기 시작한 지는 얼마 되지 않았다.
그래프는 버스와 지하철의 노선도, 출발지와 목적지를 정하면 그에 맞는 최적의 경로탐색 등에 사용된다.
그래프의 용어 및 종류
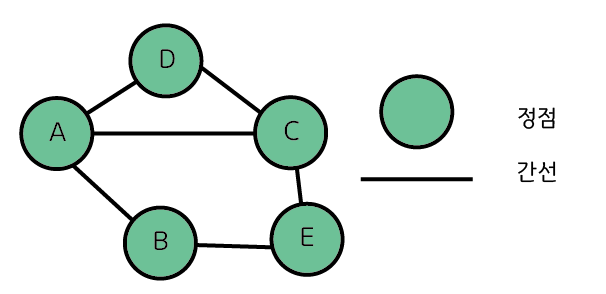
A, B, C, D, E와 같은 노드들을 정점(Vertex) 간선(Edage)는 이들 사이의 연결을 의미하며 위의 그림은 알파벳의 관계를 정점과 간선을 이용해서 표현했기 때문에 그래프라 할 수 있다. 이렇게 방향성이 없는 그래프를 무방향 그래프(Undirected Graph)라고 한다.
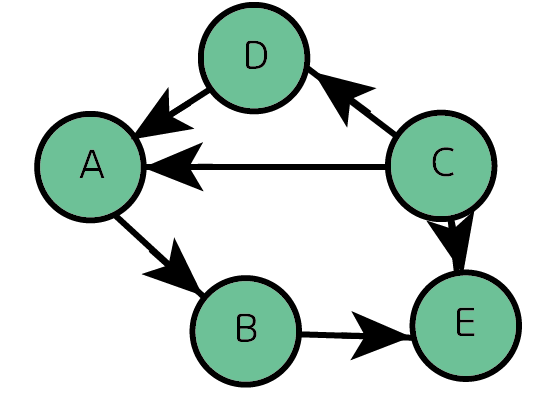
위와 같이 간선에 방향 정보가 있는 그래프를 방향 그래프(Directed Graph)라고 한다.
이러한 무방향 그래프와 방향 그래프는 간선의 연결 형태에 따라 완전 그래프(Compleate Graph)로 구분이 된다.
아래에 보이는 그림이 완전 그래프의 예이다.
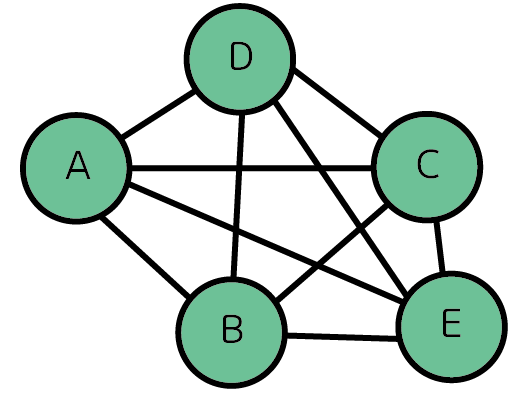
완전 그래프란 각각의 정점에서 다른 모든 정점을 연결한 그래프를 뜻한다.
동일한 그래프라고 해도 방향 그래프의 간선은 무방향 그래프의 간선의 수에 두 배가 된다.
(A----B)(B----A) 이렇게 두 간선이 필요하기 때문이다.
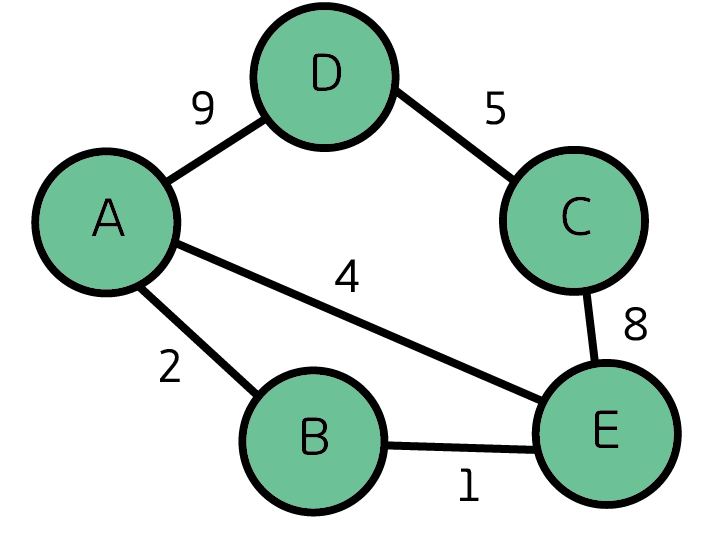
간선에 가중치 정보를 두어서 그래프를 구성할 수도 있다. 이러한 그래프를 가중치 그래프 라고 한다.
이러한 가중치 정보를 시간과 같은 정보로 사용하여 더 빠른 길을 찾는대 사용할 수 있다.
예를 들어 A에서 E로 가는 경로 중 최단 경로는
정점 A ---> 정점 E 는 4
정점 A----> 정점 B ----> E 는 3으로
밑에 경로가 더 빠르다는 것을 알수 있다.
그래프의 집합 표현
그래프는 정점과 간선으로 이루어지므로, 다음과 같이 정점의 집합과 간선의 집합으로 나누어서 표현이 가능하다.
- 그래프 G의 정점 집합 V(G)
- 그래프 G의 간선 집합 V(E)

무방향 그래프는 간선에 방향성이 없기 때문에 (A, B)와 (B, A)가 같다.
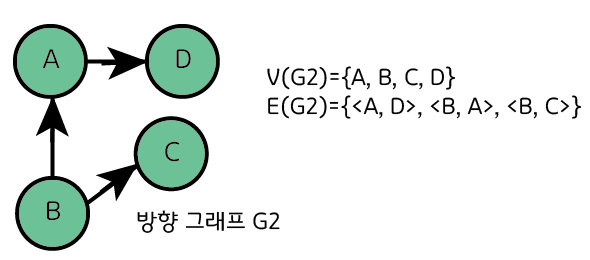
방향 그래프는 조금 방식이 다르다. 예를 들어 정점 A가 정점 C를 가리키는 직선이 있다고 하면
표현 방법은 <A, C>이다. 쉽게 말하면 시작점이 왼쪽 끝점이 오른쪽이다.
그래프를 구현하는 두 가지 방법
그래프를 구현하는 방법도 배열을 이용하는 방법과 연결 리스트를 이용하는 방법으로 나뉜다. 하지만 그래프에서는 이들 각각을 다음과 같이 부른다.
- 인접 행렬(adjacent matrix) 기반 그래프 정반 행렬을 활용
- 인접 리스트(adjacent list) 기반 그래프 연결 리스트를 활용

위와 같이 정점이 4개이면 가로세로 길이가 4인 2차원 배열을 선언한다. 그리고 두 정점이 연결되어 있으면 1 아니면 0으로 표시를 한다. 간선에 방향성이 없기 때문에 하나의 간선에 대해서 두 개의 지점을 1로 표시해야 해야 한다. 예를 들어 [M][N]가 1로 표시되면 [N][M]도 1이 되어야 한다. 이렇기 때문에 대각선 기준으로 대칭을 이룬다.

무방향 그래프와 다르게 A에서 C로 가는 간선만 표시를 하였다. 차이는 이것이 전부이며 무방향 그래프와 다르게 대칭을 이루지 않는다.

각각의 정점은 자신과 연결된 정점의 정보를 가지기 위해 각자의 연결 리스트를 가진다. 그리고 각각의 정점에 연결된 간선의 정보는 각자의 연결 리스트에 저장을 한다.

방향 그래프에서는 각 정점 별로 가리키는 정보만을 연결 리스트에 담기 때문에 무방향 그래프에 비해 추가되는 노드의 수가 반으로 줄어든다.
그래프의 탐색 방법
그래프의 탐색 방법은 너비 우선 탐색(BFS)와 깊이 우선 탐색(DPS)가 있다. 이 두 가지는
아래에 글을 작성하였다.
너비 우선 탐색(Breadth First Search)
소스코드
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
|
#pragma once
#include"pList.h"
template<class T>
class pGraph {
private:
int numv_;
int nume_;
pList<T>* list_;
public:
pGraph() :numv_(0), nume_(0), list_(nullptr) {}
void InitData(int nv) {
list_ = new pList<T>[nv];
numv_ = nv;
nume_ = 0;
}
void DestoryData() {
if (list_ != nullptr) {
delete[] list_;
}
}
void AddEage(T fromV, T toV) {
list_[fromV - 65].InitNode(toV);
list_[toV - 65].InitNode(fromV);
++nume_;
}
void DisPlay()const {
for (int i = 0; i < numv_; ++i) {
std::cout << static_cast<char>(i + 65) << ": ";
list_[i].DisplayNode();
}
}
};
|
후기

인접 리스트를 사용해서 그래프를 구현하였다. 탐색은 전에 구현했기 때문에 연결된 노드만 출력되는 정도에서 마무리를 하였고 리스트에 사용된 연결 리스트는 연결 리스트(Linked List)에서 작성하였다.
트리와 그래프를 그림으로 설명하다 보니 일러스트 실력만 느는 거 같다.
출처 및 레퍼런스
Wiki: https://ko.wikipedia.org/wiki/그래프_(자료_구조)
Book: 윤성우의 열혈자료구조
그림: 본인
'자료구조 알고리즘 > 그래프(Graph)와 트리(Tree)' 카테고리의 다른 글
| [자료구조] 이진 검색트리(Binary Search Tree) (0) | 2020.01.14 |
|---|
