알고리즘 개요 및 소개

| 시간 복잡도 | O(|E|+|V| log |V|) |
| 장점 | 최단 거리를 알 수 있다. |
| 단점 | 음의 경우의 수를 포함하지 않는다. |
다익스트라 알고리즘, 벨만-포드 알고리즘, 사이클이 없는 그래프의 최단경로 알고리즘은 하나의 시작 정점으로부터 다른 모든 정점까지의 최단경로를 구한다. 임의의 두 정점 간에 경로가 존재하지 않으면 이 경로의 길이는 INFINITE(무한)으로 정의한다. 또 두 정점 사이에 간선이 없으면 가중치가 무한인 간선이 있다고 간주한다.
다익스트라 알고리즘은 간선에 음의 가중치를 허용하지 않는대 그 이유는 시작점에서 그 정점까지의 최단 거리는 계산이 끝났다는 확신을 가지고 더하기 때문이고 만약 이후에 더 짧은 경로가 존재한다면 다익스트라 알고리즘의 논리가 깨지기 때문이다.
탐색 방법
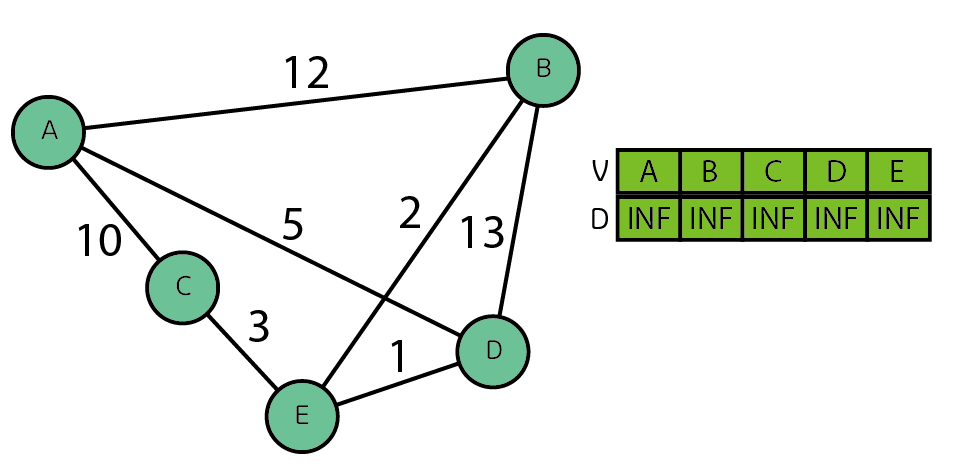
먼저 모든 정점은 아직 방문하지 않았기 때문에 INF로 처리한다.
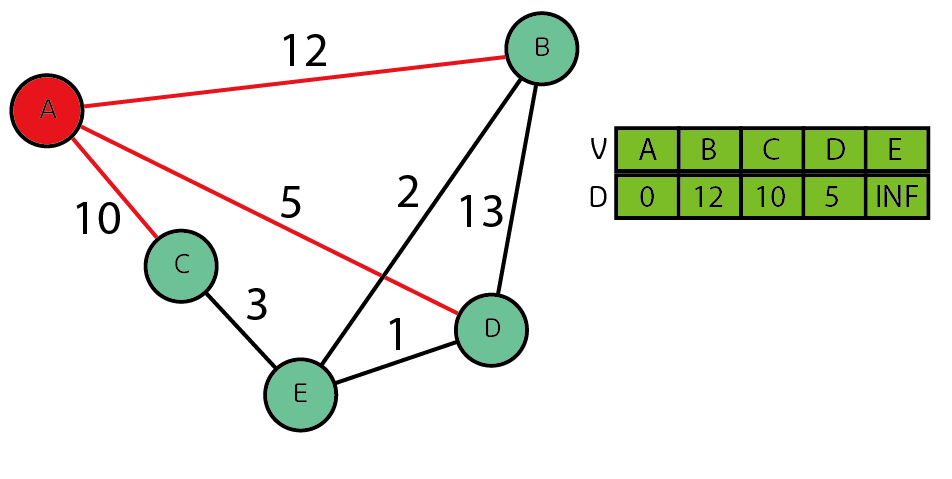
A노드를 시작 노드로 하고 처음에 연결된 모든 노드를 방문하고 그 노드의 가중치가 더 작다면 해당하는 값으로 바꾼다. 여기서는 모두 INF이기 때문에 값이 바뀌게 된다.
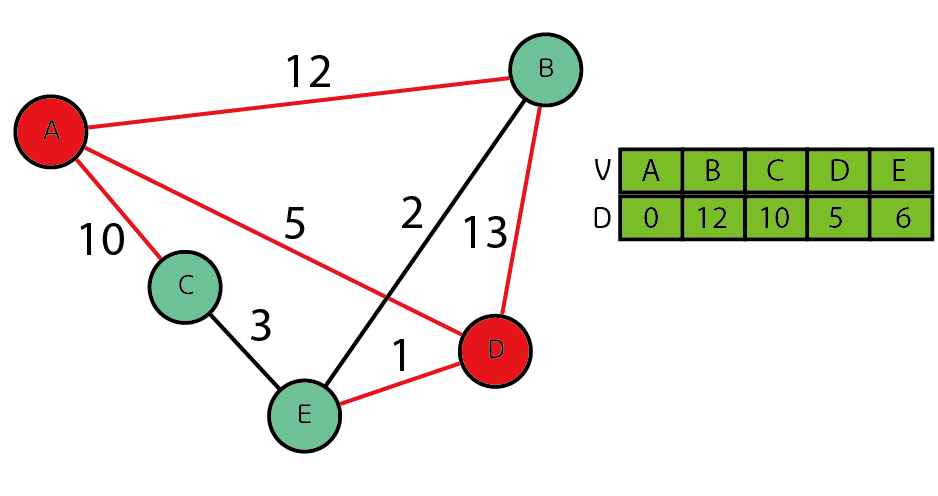
그 후 방문하지 않은 노드 중에서 가장 가중치가 낮은 노드를 선택한다 여기에서는 D를 선택하였고 똑같이 D에 연결된 노드를 방문한다.
여기서 E의 가중치 값이 6으로 바뀌었는대 기존 A-D(5)에 D-E(1)을 더한 값인 6이 들어가게 된다.

그 후 방문하지 않는 노드들 중에서 가장 가중치가 낮은 E노드를 방문한다.
여기서 B노드의 가중치는 12이지만 A-D-E 노드를 거치는 과정에서 8이라는 더 작은 숫자가 나왔기 때문에 바꾼다. C노드도 동일한 이유로 9로 값이 바뀐다.

C와 B 노드는 인접노드들 중 방문하지 않는 노드가 없기 때문에 그대로 종료된다.
소스코드
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
|
#include<iostream>
#include<vector>
#include<queue>
constexpr int INF = 2147483647;
constexpr int MAX_V =5;
enum NODE{A=0,B,C,D,E};
class Node {
public:
int v_;
int distance_;
Node():v_(0), distance_(0) {};
Node(int v, int distance) :v_(v), distance_(distance) {};
constexpr bool operator<(const Node& rhs)const{
return distance_ > rhs.distance_;
}
};
std::vector<Node>v[MAX_V];
int distance[MAX_V];
void Dijkstra(int started) {
std::priority_queue<Node> queue; //가장 작은 간선치만 꺼내기 위해 사용
distance[started] = 0;
queue.emplace(Node{ started, 0 });
while (queue.empty() == false) {
auto top = queue.top();
queue.pop();
int n = top.v_; //노드
int d = top.distance_; //거리
//해당 노드와 연결된 노드의 값을 갱신한다.
for (auto node : v[n]) {
int aroundNode = node.v_;
int aroundDistance = node.distance_ + d;
//현재 노드의 거리값이 더 작다면 갱신한다.
if (aroundDistance <= distance[aroundNode]) {
distance[aroundNode] = aroundDistance;
queue.emplace(Node{ aroundNode, aroundDistance });
}
}
}
}
int main() {
v[A].emplace_back(Node{ B,12 });
v[A].emplace_back(Node{ C,10 });
v[A].emplace_back(Node{ D,5 });
v[B].emplace_back(Node{ A,12 });
v[B].emplace_back(Node{ D,13 });
v[B].emplace_back(Node{ E,2 });
v[C].emplace_back(Node{ A,10 });
v[C].emplace_back(Node{ E,3 });
v[D].emplace_back(Node{ A,5 });
v[D].emplace_back(Node{ B,13 });
v[D].emplace_back(Node{ E,1 });
v[E].emplace_back(Node{ B,2 });
v[E].emplace_back(Node{ C,3 });
v[E].emplace_back(Node{ D,1 });
for (int i = 0; i < MAX_V; ++i)
distance[i] = INF;
Dijkstra(A);
for (int i = 0; i < MAX_V; ++i) {
std::cout << static_cast<char>('A'+i)<<" Distance: "<<distance[i]<< std::endl;
}
}
|

후기
다익스트라 알고리즘을 구현해보았다. 생각보다 알고리즘이 간단해서 놀랐다. 음의 가중치를 포함하지 않는 알고리즘이라는 단점이 있지만 현실에서는 음의 가중치가 없기 때문에 실용적인 알고리즘이기도 하다.
길 찾기에 마지막은 A* 알고리즘을 해볼 예정이며 이걸 게임에 적용까지 해보는게 탐색 알고리즘의 최종 목표이다.
출처 및 레퍼런스
Wiki: https://ko.wikipedia.org/wiki/데이크스트라_알고리즘
Book: 쉽게 배우는 알고리즘 관계 중심의 사고법 저) 문병로
그림: 본인
*2020.04.05
code를 Color Scripter로 변경
관련 글
[자료구조 알고리즘/탐색 알고리즘(Search)] - [알고리즘] 깊이 우선 탐색(Depth First Search)
[자료구조 알고리즘/탐색 알고리즘(Search)] - [알고리즘] 너비 우선 탐색(Breadth First Search)
'자료구조 알고리즘 > 탐색 알고리즘(Search)' 카테고리의 다른 글
| [알고리즘] A* 알고리즘 (0) | 2020.08.24 |
|---|---|
| [알고리즘] 백 트래킹(Backtracking) (0) | 2020.03.31 |
| [알고리즘] 합집합 찾기(Union-Find) (0) | 2020.02.14 |
| [알고리즘] 최소 비용 신장 트리(Minimum Cost Spanning Tree) (0) | 2020.02.11 |
| [알고리즘] 깊이 우선 탐색(Depth First Search) (0) | 2020.02.03 |



