알고리즘

최소 비용 신장 트리 또는 최소 신장 트리는 아래와 같은 특징을 같는다.
- 그래프의 모든 정점이 간선에 의해서 하나로 연결되어 있다.
- 그래프 내에서 사이클을 형성하지 않는다.
이러한 최소 비용 신장 트리는 전기회로 구성이나 네트워크 구축 등에 사용된다.
사이클(Cycle)을 형성하지 않는 그래프

정점 B에서 D로 가는 모든 경로는 4가지 이다. 그리고 위의 네 경로와 같이 동일한 간선을 중복하여 포함하지 않는 경로를 단순 경로(Simple Path)이라 한다.
B-A-C-B-A-D 이 경로는 단순 경로가 아니다.
그러면 이 경로는 단순 경로일까? A-B-C-A
정점 A가 두 번 등장하지만 단순 경로가 맞다. 중복된 간선이 포함되지 않았기 때문이다. 즉, 이는 경로의 시작과 끝이 같은 단순 경로이다. 이렇듯 단순 경로이면서 사직과 끝이 같은 경로를 가리켜 사이클(Cycle)라고 한다.
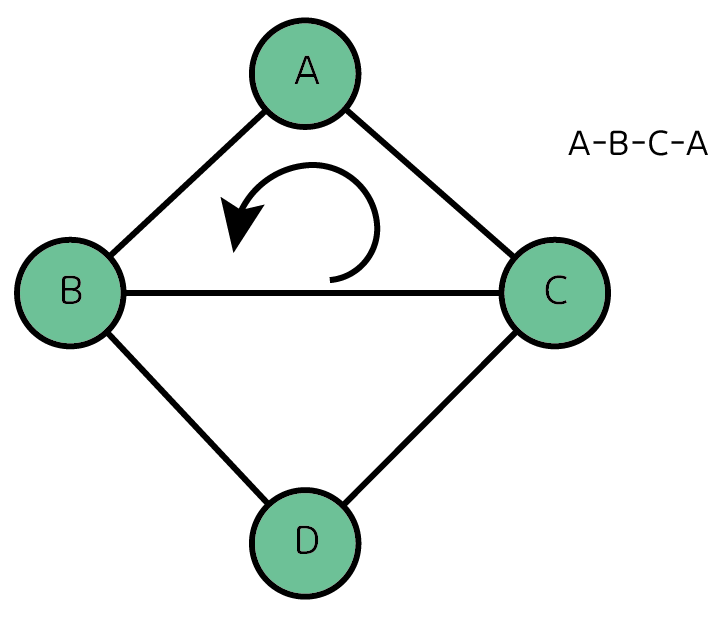
위와 같은 그림이 사이클이다.

반대로 위와 같은 그림이 사이클을 형성하지 않는 그래프이며 이러한 그래프를 90~180도 회전시키면 트리 형태가 되기 때문에 사이클을 형성하지 않는 그래프들을 가리켜 신장 트리(spanning tree)라고 한다.
최소 비용 신장 트리의 알고리즘
최소 비용 신장 트리의 구성에 사용되는 대표적인 알고리즘 두 가지는 다음과 같다.
크루스칼(kruskal) 알고리즘
- 가중치를 기준으로 간선을 정렬한 후에 *MST가 될 때까지 간선을 하나씩 선택 또는 삭제해 나가는 방식
프림(Prim) 알고리즘
- 하나의 정점을 시작으로 MST가 될 때까지 트리를 확장해 나가는 방식
MST: 최소 비용 신장 트리
크루스칼(Kruskal) 알고리즘
크루스칼 알고리즘의 핵심은 가중치를 정렬한다는 것에 있다. 이 정렬방법은 오름차순과 내림차순 두 가지 방법이 있다.
| 오름차순 모델 |
오름차순 모델은 가중치가 작은 간선부터 하나씩 선택하는 방법이다.

먼저 가중치가 가장 낮은 1번 간선을 선택한다.

간선을 추가하다 9번 간선을 추가하려는 순간 그래프에 사이클이 형성되기 때문에 9번 간선은 선택을 하지 않고 다음 간선으로 넘어간다.

MST는 하나의 특징을 가지고 있는대 바로 정점의 수는 간선의 수+1이라는 것이다.
위 그림도 간선의 수는 6개이며 노드는 간선+1개인 7개이기 때문에 최종 모습이라고 볼 수 있다.
위 알고리즘의 흐름의 핵심은 다음과 같다.
- 가중치를 기준으로 간선을 오름차순으로 정렬한다.
- 낮은 가중치의 간선부터 시작해서 하나씩 그래프에 추가한다.
- 사이클을 형성하는 간선은 추가하지 않는다.
- 간선의 수가 정점의 수보다 하나 적을 때 MST는 완성된다.
| 내림차순 모델 |
내림차순 모델은 높은 간선부터 하나씩 삭제해 나아가는 방법이다.

가중치가 가장 높은 20부터 차례대로 삭제를 진행한다.
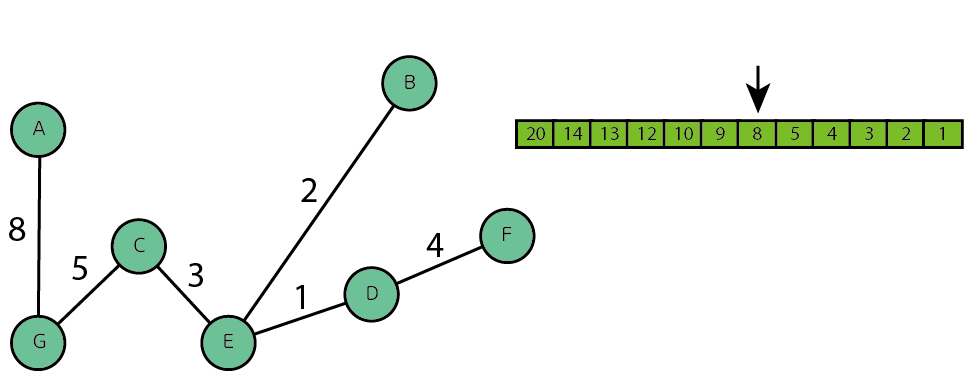
삭제를 진행하던 중 8번째 간선을 삭제하면 다음과 같은 문제가 발생한다.
"가중치가 8인 간선을 삭제하면 정점 A와 정점 G는 어떤 경로를 통해서든 닿지 않는다."
MST의 모든 정점은 간선에 의해서 하나로 연결되어야 하기 때문에 이러한 경우에는 삭제를 하지 않고 넘어간다.
그리고 이를 통해 다음과 같은 결론을 내릴 수 있다.
"두 정점이 다른 경로를 통해서도 연결되어 있는 경우에만 해당 간선을 삭제할 수 있다.

위 알고리즘의 흐름의 핵심은 다음과 같다.
- 가중치를 기준으로 간선을 내림차순으로 정렬한다.
- 높은 가중치의 간선부터 시작해서 하나씩 그래프에서 제거한다.
- 두 정점을 연결하는 다른 경로가 없을 경우 해당 간선은 제거하지 않는다.
- 간선의 수가 정점의 수보다 하나 적을 때 MST는 완성된다.
소스코드
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
|
#include<iostream>
#include<queue>
#include<list>
#include<stack>
enum NodeName { A, B, C, D, E, F, G };
class Edge {
private:
public:
int v1_; //간선이 연결하는 첫 번째 정점
int v2_;// 간선이 연결하는 두 번째 정점
int weight_; //가중치 정보
Edge() :v1_(0), v2_(0), weight_(0) {}
Edge(int v1, int v2, int weight) :v1_(v1), v2_(v2), weight_(weight) {}
constexpr bool operator<(const Edge& rhs) const {
return weight_ < rhs.weight_;
}
};
class Graph {
private:
int numV_;
int numE_;
bool* visited_;
std::list<int>* nodelist_;
std::priority_queue<Edge>queue_;
private:
void EraseNode(const int v1, const int v2) {
auto iter = std::find_if(nodelist_[v1].cbegin(), nodelist_[v1].cend(), [&](auto& rhs) {
return rhs == v2;
});
nodelist_[v1].erase(iter);
}
void RecoveryNode(const int v1, const int v2) {
nodelist_[v1].push_back(v2);
nodelist_[v2].push_back(v1);
}
bool IsLastNode(const int v1, const int v2) {
for (int i = 0; i < numV_; ++i)
visited_[i] = false;
std::stack<int>dfs;
visited_[v1] = true;
//해당 노드에서 갈 수 있는 모든 경로를 스택에 넣는다.
dfs.pop();
for (auto i : nodelist_[node]) {
if (visited_[i] == false) {
//만날 수 있는 경로가 있다.
if (i == v2)
return false;
visited_[i] = true;
}
}
}
//못만나면 지운거를 취소해줘야 한다.
return true;
}
public:
Graph() :numV_(0), numE_(0), nodelist_(nullptr),visited_(nullptr) {}
void GraphInit(int nv) {
numV_ = nv;
numE_ = 0;
nodelist_ = new std::list<int>[nv];
visited_ = new bool[nv] {true};
}
void AddEage(Edge&& newEdge) {
nodelist_[newEdge.v1_].push_back(newEdge.v2_);
nodelist_[newEdge.v2_].push_back(newEdge.v1_);
++numE_;
}
void KruskalMST() {
/*
최소신장트리 조건
1. 사이클이 없어야한다.
2. 모든 노드는 하나의 간선을 가진다.
3. 정점의개수는 간선의개수+1이다.
*/
Edge recovery[20];
int recovery_index = 0;
//정점의 개수가 간선개수 +1이면 그만
while (numV_ != numE_ + 1) {
//가장 가중치가 높은 간선을 꺼낸다.
int v1 = topNode.v1_;
int v2 = topNode.v2_;
EraseNode(v1, v2);
EraseNode(v2, v1);
//지웠더니 만날 수가 없다.
if (IsLastNode(v1, v2)) {
RecoveryNode(v1, v2);
RecoveryNode(v2, v1);
recovery[recovery_index++] = topNode;
}
//문제가 없다.
else {
--numE_;
}
queue_.pop();
}
for (int i = 0; i < recovery_index; ++i)
queue_.push(recovery[i]);
}
void DisplayGraph() {
for (int i = 0; i < numV_; ++i) {
std::cout << static_cast<char>(65 + i) << "에 연결된 정점:";
for (auto iter : nodelist_[i]) {
std::cout << static_cast<char>(65 + iter) << " ";
}
std::cout << "\n";
}
std::cout << "\n\n";
int result=0;
while (queue_.empty() == false) {
auto topnode = queue_.top();
result += topnode.weight_;
queue_.pop();
std::cout << "(" << static_cast<char>(65 + topnode.v1_) << "-"
<< static_cast<char>(65 + topnode.v2_) << ")," << " w:" << topnode.weight_ << "\n";
}
std::cout << "Total Weight: " << result<<"\n";
}
void GraphDestory()const {
if (nodelist_ != nullptr)
delete[] nodelist_;
}
};
int main() {
Graph graph;
graph.GraphInit(7); //A,B,C,D,E,F,G,H
graph.AddEage(Edge{ A,B,12 });
graph.AddEage(Edge{ A,C,10 });
graph.AddEage(Edge{ A,D,20 });
graph.AddEage(Edge{ A,G,8 });
graph.AddEage(Edge{ B,D,13 });
graph.AddEage(Edge{ B,E,2 });
graph.AddEage(Edge{ B,F,14 });
graph.AddEage(Edge{ C,G,5 });
graph.AddEage(Edge{ C,E,3 });
graph.AddEage(Edge{ D,F,4 });
graph.AddEage(Edge{ D,E,1 });
graph.AddEage(Edge{ E,G, 9 });
graph.KruskalMST();
graph.DisplayGraph();
graph.GraphDestory();
}
|
후기
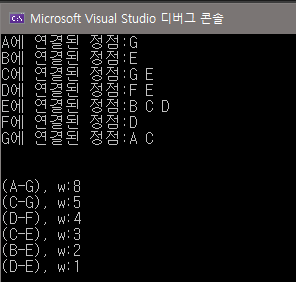
크루스칼 알고리즘 중 내림차순 모델을 코드로 구현하였다. 사용된 자료구조는 리스트, 우선순위 큐, 그래프가 사용됐다.
오람차순의 경우에는 사이클이 형성되는지를 Union-Find라는 알고리즘을 통해서 찾아봐야 해서 내림차순 모델을 선택하였다 이 모델은 DFS를 사용해서 노드가 끊겨있는지 여부를 확인 할 수 있다.
출처 및 레퍼런스
Wiki: https://en.wikipedia.org/wiki/Minimum_spanning_tree
Book: 윤성우 자료구조
그림: 본인
관련글
20.04.22
소스코드 -> color Scripter, 글자 폰트 및 색상 변경
'자료구조 알고리즘 > 탐색 알고리즘(Search)' 카테고리의 다른 글
| [알고리즘] 다익스트라 알고리즘(Dijkstra algorithm) (0) | 2020.02.25 |
|---|---|
| [알고리즘] 합집합 찾기(Union-Find) (0) | 2020.02.14 |
| [알고리즘] 깊이 우선 탐색(Depth First Search) (0) | 2020.02.03 |
| [알고리즘] 너비 우선 탐색(Breadth First Search) (0) | 2020.01.31 |
| [알고리즘] 이진 탐색(Binary Search) (1) | 2020.01.12 |



